추정과 구간 추정
점추정
모수를 특정한 수치로 표현하는 것
추정
추정치 : 모수를 추정하기 위해 선택된 표본을 대상으로 구체적으로 도출된 통계량
추정량 : 표본에서 관찰된 값으로 추정치를 계산하기 위한 도출 함수
바람직한 점 추정량의 조건
불편성 : 추정량이 모수와 같아야 한다.
일치성 : 표본의 크기가 모집단 규모에 근접해야 한다.
유효성 : 추정량의 분산이 최소값이어야 한다.
충분성 : 표본이 모집단의 대표성을 가져야 한다.
구간추정
모수를 최소값과 최대값의 범위로 추정하는 것
일정한 크기의 신뢰수준으로 모수가 특정한 구간에 있을 것 이라고 선언
구해진 구간을 신뢰구간이라고한다.
표본의 크기가 커질 수록 구간이 좁아진다. ( 정보가 많을수록 추정량이 더 정밀하다는 것을 의미 )
신뢰구간 95% 라는 뜻은
확률의 개념이 아니라 100번 중에 95번은 맞아떨어진다는 말이다.
100개 중에 95개는 구간 안에 모수가 포함되어있다.
신뢰수준이 95% 라면 유의 확률은 0.05
신뢰구간

신뢰도 90%에서의 구간추정
표본평균(X바) = 500, SE = 100 , z=1.64 이므로 다음과 같이 구할 수 있다.
500 - 1.64 * 100 <= u <= 500 + 1.64 * 100
336 <= u <= 664
신뢰도 95%에서의 구간추정 ( 보통 95%로 설정)
표본평균(X바) = 500, SE = 100 , z=1.96 이므로 다음과 같이 구할 수 있다.
500 - 1.96 * 100 <= u <= 500 + 1.96 * 100
304 <= u <= 696
신뢰도가 높아질 수록 범위(신뢰구간)가 넓어짐
모집단의 표준편차를 아는 경우 신뢰구간을 구하는 방법

모집단의 표준편차를 모르는 경우 신뢰구간을 구하는 방법

대립 가설(H1)
입증하여 주장하고자 하는 가설
귀무가설(H0)
- 대립 가설의 반대 가설
기본적으로 검정을 하게 될 때 귀무가설을 기각함으로써 대립 가설을 채택하게 됨
ex) "반 학생들의 키 평균이 160cm 다"가 가설일 때 이 가설은 귀무가설
이 가설이 맞느냐 틀리냐에 따라서 다양한 주장을 할 수 있게 된다.

- 표본을 조사했을 때 표본 평균이 170일 때는 귀무가설일 것 같다 ( 신뢰 수준 안에 있다. )
- 다른 표본을 조사했을 때 표본 평균이 180일 때는 귀무가설을 기각하게 된다. ( 신뢰 수준을 벗어나 있다. )
오류의 종류
1종 오류 ( a ) = 유의수준
귀무가설이 맞을 때 , 귀무가설을 기각하는 오류.
맞는데 틀리게 하는 경우
2종 오류 ( b )
귀무가설이 틀렸을 때 귀무가설을 기각하지 않는 오류
틀린데 맞다고 하는 경우
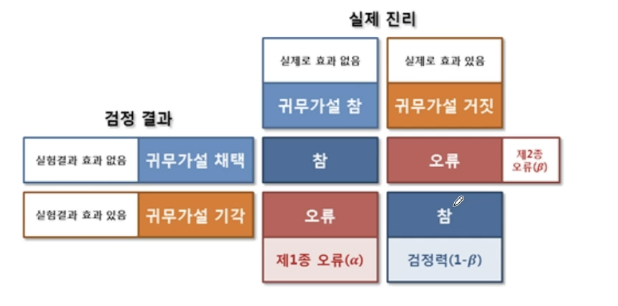
두 가지 오류는 서로 상충관계(하나가늘면 하나가 감소) 가설 검정에서는
1종오류를 고정하고 제2종 오류가 최소가 되도록 기각역 설정
검정 통계량
- 우리의 자료로부터 계산하게 되는 값
- 검정 통계량은 모수를 추정하고자 하는 것
- 귀무가설을 기각을 할지 말지는 모수로부터 검정통계랑이 얼마나 떨어져 있는데 따라서 판단한다.
표본에서 구해낼 수 있는 함수, 이 값을 기준으로 귀무가설 기각 여부를 결정
기각역
검정 통계량이 취하는 구간 중 귀무가설을 기각하는 구간.
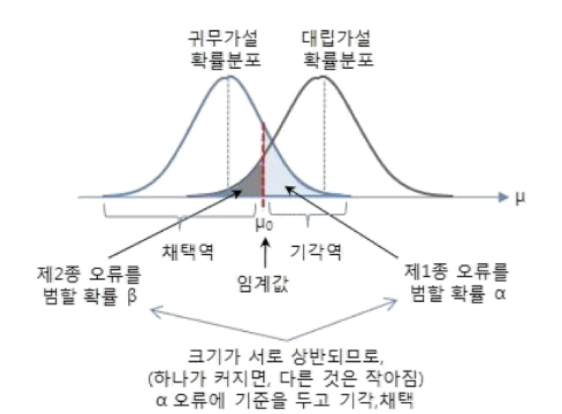
검정통계량 , 기각역
단측검정
H1 : u > u0
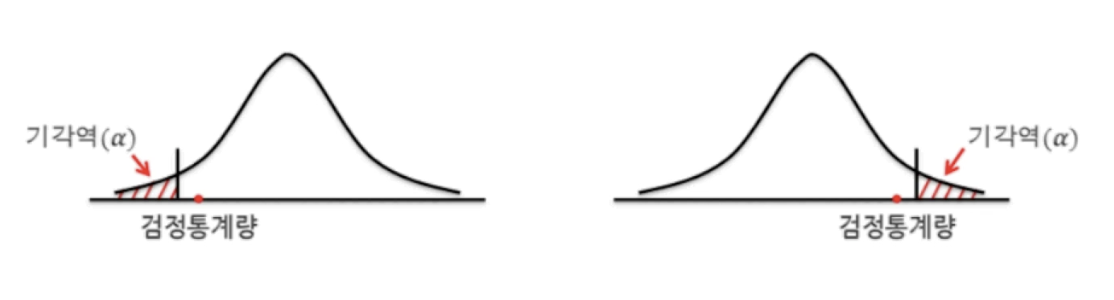
양측검정
H1 : u != u0
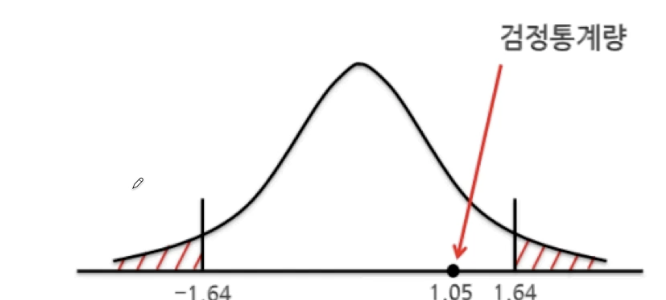
유의확률(P-value)
주어진 검정통계량값을 기준으로 해당 값보다 대립가설을 더 선호하는
검정통계량 값이 나올 확률.
이 값(p-value) 이 유의수준(a) 보다 낮으면 귀무가설을 기각.

귀무가설을 기각을 할 수 있는 두 가지 방법
- p-value 가 유의수준보다 낮을 경우
- 검정통계량의 값이 기각역의 위치할 경우
보통 a(유의수준)을 0.05로 많이 지정을 하게 되고
p-value (유의확률)가 0.05보다 낮으면 귀무가설을 기각하고 대립가설을 채택한다.
가설검정 순서
| 가설수립 | 귀무가설과 대립가설을 수립 |
| 유의수준 결정가설수립 | 귀무가설과 대립가설 중 어떤 가설을 채택할 것인지 판단하는 유의수준(a)를 결정 |
| 기각역 설정 | 단/양측검정 정해 기각역 설정 |
| 통계량 계산 | 통계량 계산 후 유의수준과 비교 |
| 의사결정 | 어떤 가설을 채택할 것인지를 결정. |
비모수 검정
- 모집단이 데이터가 정규분포, 등분산 가정 따르고 있지 않을 때
- 이상치를 포함한 분석을 실시하고 싶을 때
- 얻어진 데이터가 순서척도 일때
- 자료가 추출된 모집단의 분포에 대해 아무런 제약을 가하지않고 검정을 실시하는 검정 방법
- 관측값들의 순위나 두 관측값 사이의 부호 등을 이용해 검정한다.
- 모집단의 특성을 몇 개의 모수로 결정하기 어려우며 수많은 모수가 필요할 수 있다.
맨 휘트니 U 검정
순위척도를 가진 집단이거나 집단의 표본수가 적을 때 두 집단 차이를 분석하는 방법
단계1 가설 수립
귀무가설: A,B 무게 차이는 없다.
대립가설: A,B 무게차이가 있다.
단계2: 두 그룹으로 정렬된 무게에 등수부여
단계3: 그룹별 U값 계산
단계4: U값을 이용한 차이검정
단계5 :p값, 유의수준 비교하여 가설 채택 또는 기각
독립변수와 종속변수가 둘다 범주형일때 대표적으로
비모수적검정(카이제곱검정)을 사용하게된다.
이러할 때 검정의 종류
적합도검정
- 관측값들이 어떤 이론적 분포를 따르고 있는 지 ( 이론치와 관측치가 차이가 있는지 없는지)
독립성검정
- 서로 연관이 있는지 서로 독립인지 아닌지
ex) 흡연량과 음주량
동질성검정
관측값들이 정해진 범주내에서 서로 비슷한지
ex) 흡연량과 음주량이 동일한 분포인가
'Data Science > ADsP' 카테고리의 다른 글
| [ADsP]3과목 - 3장.상관분석 및 다차원분석, 주성분분석,시계열 예측 (0) | 2020.05.26 |
|---|---|
| [ADsP]3과목 - 2장.정규성 검정,단순회귀,결정계수,다중공선성,설명변수 선택 (0) | 2020.05.25 |
| [ADsP]3과목 - 2장.확률 및 확률분포 , 표본의 분포 (0) | 2020.05.25 |
| [ADsP]3과목 - 1장. reshape패키지,sqldf,data.table함수 , 결측값 처리와 이상값 검색 (0) | 2020.05.25 |
| [ADsP]3과목 - 1장. 데이터마트와 apply함수,plyr 패키지 (0) | 2020.05.23 |
![[ADsP]3과목 - 2장.점추정과 구간추정 , 가설검정 , 비모수 검정](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FBCTaO%2FbtqEo7GCX6a%2FAAAAAAAAAAAAAAAAAAAAAB3xW6wt6iNB-3jV73T2sa_4UBOt3tD8r5p6WU-1WNna%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DKMPDVNNUDvCT%252FoxN3qDQAB9Tmmw%253D)