회귀분석이란?
회귀 분석에 들어가기 전에
먼저 지도 학습(Supervised Learnig)과 비지도 학습(Unsupervised Learning)에 대해서 알아봅시다.
2020/03/19 - [데이터 사이언스/머신러닝] - [기계학습] 2. 지도 학습과 비지도 학습
[기계학습] 2. 지도학습과 비지도학습
지도학습(supervised learning) Y = f (x) 에 대하여 입력변수 (X) 와 출력변수 (Y) 의 관계에 대하여 모델링하는 것 (Y에 대하여 예측 또는 분류하는 문제) 회귀 (regression) : 입력 변수 X에 대하여 연속형 출..
acdongpgm.tistory.com
회귀분석은 지도 학습에 한 종류이며
Y = f(x)에 대하여 입력 변수(X)와 출력 변수 (Y)의 관계에 대하여 모델링하는 것이다.
회귀분석은
정의 : 입력 변수인 X의 정보를 활용하여 출력 변수인 Y를 예측하는 방법.
회귀분석 중 간단한 방법으로는 선형 회귀분석이 있으며, 이를 바탕으로 더 복잡한 비선형 회귀분석이 개발됨.

* 대부분의 분류 모델 (SVM , Decistion Tree 등)로도 회귀가 가능함.
단순 선형 회귀분석

입력 변수가 X , 출력 변수가 Y 일 때, 단순 선형 회귀의 회귀식은 검은 선으로 나타낼 수 있음.
B0는 절편(intercept) , B1 은 기울기(slope)이며 합쳐서 회귀계수(coefficients)로도 불림
e 은 오 차 항 , 신만이 알 수 있는 오차

검은 점 : 모집단의 데이터
빨간 점 : 학습 집합의 데이터
실제 B0와 B1은 구할 수 없는 계수로 데이터(학습 집합)를 통해 이 둘을 추정해서 사용
* 가정

-
우리가 알고 싶은 식

-
우리가 추정해야 하는 식

모자를 씌워서 추정한다. 오 차 항은 0으로 가정한다.
어떻게 추정할까?
Q : 여러 개의 직선 중 가장 좋은 직선은?

위에 많은 직선 중에 가장 좋은 직선을 뭘까요 라고 물어보면 대부분
한 가지 직선으로 대답을 하게 된다.
Why?
- 데이터 분포의 가운데를 이 직선이 지나고 있기 때문에
- 데이터 안에 있는 이 직선의 오차가 가장 작아지는 것 같아서.
결론 : 직선과 데이터의 차이가 평균적으로 가장 작아지는 직선이 가장 좋은 직선이다.
가장 Y를 잘 설명해주는 직선이다.
회귀계수 추정
회귀계수는 : 절편 + 기울기
실제 값과 우리가 추정한 값의 차이가 적으면 적을수록 좋은 것

실제 값과 우리가 추정한 값의 차이를 잔차(residual)라고 하며 이를 최소화하는 방향으로 추정
잔차를 그림으로 나타내면 아래와 같음

잔차의 제곱합을 최소화시키는 방향으로 추정을 하게 된다.
잔차의 제곱을 하는 이유는 양수와 음수를 양수로 통일시키기 위해서 ( 제곱을 하면 음수가 양수가 됨 )
잔차의 제곱합(SSE: Error sum of Squares)은 아래와 같이 표현 가능

굳이 잔차의 제곱합을 최소화시키는 이유 (Why?)
"Q1 : 만약 잔차의 합이 0 이 되게 한다면 어떨까?"
잔차의 합이 0 이 되는 해는 무수히 많음 ( 유일한 해를 찾지 못함 )
해가 많아서 그중 가장 나은 것을 판별할 수가 없음


"Q2 : 잔차의 절댓값을 미분하면 어떨까?"
잔차의 절댓값의 합은 미분이 불가능한 형태


"Q3 : 결과적으로 잔차의 제곱 합을 쓰는 이유는?"
잔차의 제곱 합은 미분이 가능한 형태로 유일한 해를 찾을 수 있음

- 2차 함수의 형태로 되어있기 때문에 Bo과 B1로 미분이 가능하다.
- 0이 되는 지점(SSE가 최소화되는 지점)을 찾으면 그것이 바로 가장 적합한 회귀모델이 된다.
회귀 계수의 추정



식이 2개 미지수가 2개이기 때문에 연립방정식을 풀 수가 있다.
회귀계수를 추정하는 방법 = 편미분 하여 연립방정식을 푸는 것
Matrix 미분 활용 회귀분석에 적용
모델 :

Y = B1x1 + B2x2..... + Bnxn
어떠한 값을 곱한 다음에 더해서 Y를 찾게 됨.
행렬(Matrix)의 식은 Y = B1x1 + B2x2..... + Bnxn이고 이것을 간단하게 Y = Xb + e로 표기한다.
" ex : 인기도를 추정하는 방법 "
B = 몸무게
x = 키
일 경우 몸무게가 작고 키가 클수록 인기도(Y)가 높다.
오차 제곱합 ( 행렬 ) :

회귀분석이기 때문에 오차 제곱합이 최소가 되는 해를 구하기 위해 미분을 진행해야 한다.
B는 column vector.
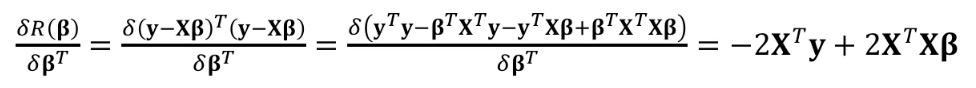
미분한 함수를 0 이 되게 하는 해를 찾음 ( 0을 대입한다. )

우리가 미분을 한 결괏값 즉, 원하는 아웃풋(output)이 column 벡터가 되도록 하기 위해서
미분을 할 때 B로 하지 않고 BT ( 베타의 트랜스 포즈 ) 값으로 미분을 한다.
출처 : 패스트캠퍼스 온라인 강의 - 올인원 패키지 : 머신러닝과 데이터 분석 A-Z
'Machine learning' 카테고리의 다른 글
| [Machine Learning] 단순선형회귀분석(Simple Linear Regression) 예제 ,pandas , numpy , plot (0) | 2020.05.11 |
|---|---|
| [기계학습]회귀계수의 의미 , 희귀계수 검정 ( SST , SSE , SSR , P-value ) (0) | 2020.04.28 |
| [기계학습]과적합(overfitting)이란? (0) | 2020.03.25 |
| [기계학습]지도학습과 비지도학습 (0) | 2020.03.19 |
| [기계학습]Machine Learning의 개념 (0) | 2020.03.19 |
![[기계학습]회귀분석 , 회귀계수 추정 , Matrix 미분 활용](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbO9zqZ%2FbtqDzjvSIcJ%2FTvreyBpTj7QhkjJrVq9DQK%2Fimg.png)