회귀 계수의 해석

예시) radio 광고 예산과 매출 간의 관계
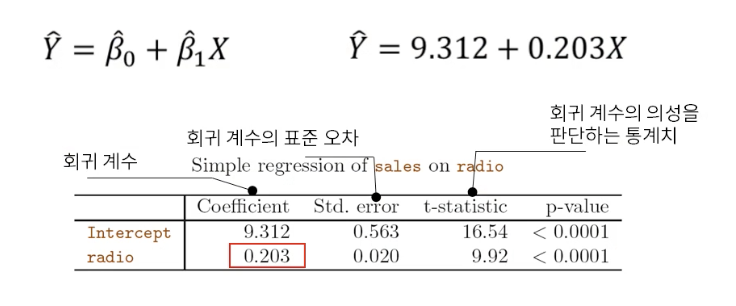
- Radio광고 예산이 1 증가할 때마다 매출은 0.2 단위만큼 증가한다.
- 그때의 유의성은 매우 높다.
잠깐!!
|
유의성이란? 데이터가 유의미한지 아닌지를 판단하는 기준 P-value를 통해 유의성 검정을 실시한다. |
Radio 광고 예산이 35 단위일 때 예상 매출액은 9.312 + 0.203*35 = 16.42 단위이다.
선형 회귀의 정확도 평가
- 선형 회귀는 잔차의 제곱합(SSE : Error sum of squares )을 최소화하는 방법으로 회귀 계수를 추정
- 즉 , SSE가 작으면 작을수록 좋은 모델이라고 볼 수 있음
- MSE(Mean Squared Error)는 SSE를 표준화한 개념

SSE 가 작아지면 MSE 도 작아짐
선형 회귀의 정확도 평가
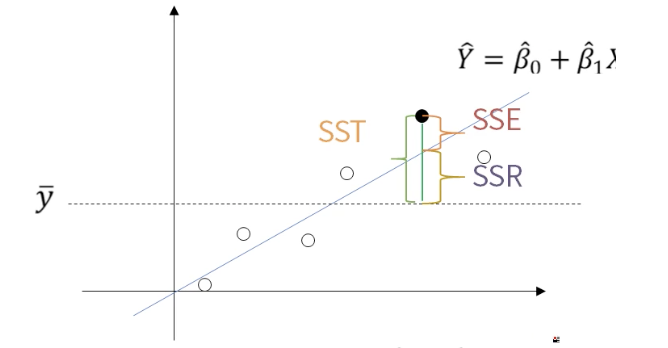
SST ( Total sum of squares )
- SSE + SSR의 합
- Y의 총 변동(SST)은 직선으로 설명 불가능한 변동 SSE와 직선으로 설명 가능한 변동 SSR로 되어있다.
SSE ( Error sum of squares )
- 회귀선에 위치한 값(추정 값)과 실제값의 차이(오차)의 제곱
- 직선으로 설명이 불가능한 변동
SSR ( Regression sum of squares )
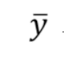
( Y바 ) : Y 의 평균을 의미한다.
- 회귀선에 위치한 값(추정값) 과 Y의 평균을 뺀 값의 제곱
- 직선으로 설명이 가능한 변동
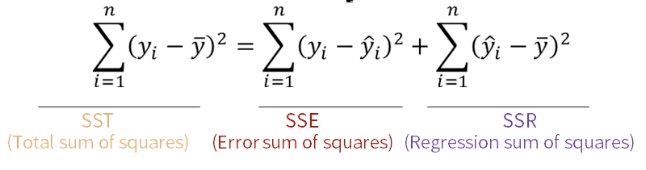
SSE 가 최소화 하는 방향으로 계산하게 되면 시그마 ei 는 0 이 된다.
시그마ei = 0 식을 만족하는 b0 , b1을 찾았기 때문


Sum of Squares는 변동성이라고 생각하면 된다.
-
직선(Regression)에 대한 변동성은 SSR
-
오차(Error)에 대한 변동성은 SSE
-
전체(Total)에 대한 변동성은 SST이다.
Degree of freedom ( 자유도 )
- 분산의 자유도는 N-1 이기 때문에 Total의 자유도와 같다.
- SSE의 자유도는 SST - SSR 이기 때문에 N-2 가 된다.
- Mean Square 은 변동성을 자유도로 나누어 준 것
선형 회귀의 정확도 평가

- Y의 총 변동(SST)은 회귀 직선으로 설명 불가능 한 변동(SSE)과 회귀 직선으로 설명 가능한 변동(SSR)으로 이루어져 있음
- R^2는 RSE의 단점을 보완한 평가지표로 0~1의 범위를 가짐
- R^2(R Squares) 은 설명력으로 입력 변수인 X로 설명할 수 있는 Y의 변동을 의미
- R^2 이 1에 가까울수록 선형 회귀 모형의 설명력이 높다는 것을 뜻함.
R^2 = 총 변동(SST) / 회귀 직선이 설명이 가능한 변동(SSR)
그러나,
* 쓸모없는 변수가 추가될 때 , 변수가 여러 개 일 때 R^2 값은 증가한다( Why? 제곱합 이기 때문에).
즉 R^2 값은 의미 없는 값이 될 수 도 있다. ( 반드시 의미 있는 값은 아니다 )

- 회귀 분석은 결국 Y의 변동성을 얼마나 독립변수가 잘 설명하느냐가 중요
- 변수가 여러 개일 때 각각 Y를 설명하는 변동성이 크면 좋은 변수 -> p-value 자연스레 낮아짐
회귀계수에 대한 검정
단순 선형 회귀분석의 검정 ( 가설 검정 )
가설검정을 사용하기 위해서 통계적인 분포가 필요함
그래서 t - 분포를 사용한다.
아래링크를 통해서 t - 분포에 대해서 알아보자!!
2020/04/01 - [데이터 사이언스/기초통계] - [기초통계] 수학적 개념 ( Z통계량 , t분포 , F분포 , 카이제곱 분포 ))
실제 모집단의 표준편차를 알 수 없기 때문에 추정을 해서 대입

단순 선형 회귀 분석의 검정
B^1의 검정
- 귀무가설 : B1 = 0 ( 회귀계수는 0이다 , 즉 변수의 설명력이 없다. )
- 대립 가설 : B1!= 0 ( 회귀계수는 0 이 아니다, 즉 변수의 설명력이 존재한다.)
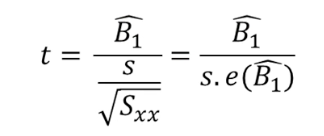
통계학에서 일반적으로 귀무가설을 기각하기가 쉽다.
회귀계수가 0 만 아니면 되기 때문에

라디오 광고와 매출
- 회귀계수(Coefficient)는 0.203이다.
- 표준오차(Std. error)는 0.020이다.
- t-통계량(t-statistic) 은 9.92 다
- p-value는 0.0001이다.
t 통계량 = 회귀계수 / 표준오차
0.203 / 0.020 = 9.92
일반적으로 t 통계량이 3 이상이면 p-value는 0에 수렴하게 된다.
p-value 가 커지려면 ( 의미가 없으려면 )
t - 통계량이 낮아지려면
표준오차가 크거나 회귀계수가 0에 가깝게 되면 p-value가 의미가 없어진다.
즉, 귀무가설을 채택하게 된다.
신문 광고와 매출
- 회귀계수(Coefficient)는 0.055이다.
- 표준오차(Std. error)는 0.017이다.
- t-통계량(t-statistic) 은 3.30 다
- p-value는 0.0001이다.
신문광고의 경우
회귀계수가 낮지만 0.055
표준오차가 낮기 0.017 때문에
0.055 / 0.017 = 3.30
t 통계량의 값이 3이 넘어간다.
그래서 p-value 가 의미가 있어지고
데이터가 유의미하다는 결론을 짓게 된다.
대립 가설 채택
b1의 신뢰구간에 0이 포함이 되면
귀무가설을 채택하고, 포함이 안되면 대립 가설을 채택하게 된다.
'Machine learning' 카테고리의 다른 글
| [기계학습] 다중 선형 회귀 분석 ( 회귀 계수 , 모델에 대한 검정 ) (0) | 2020.06.11 |
|---|---|
| [Machine Learning] 단순선형회귀분석(Simple Linear Regression) 예제 ,pandas , numpy , plot (0) | 2020.05.11 |
| [기계학습]회귀분석 , 회귀계수 추정 , Matrix 미분 활용 (0) | 2020.04.22 |
| [기계학습]과적합(overfitting)이란? (0) | 2020.03.25 |
| [기계학습]지도학습과 비지도학습 (0) | 2020.03.19 |
![[기계학습]회귀계수의 의미 , 희귀계수 검정 ( SST , SSE , SSR , P-value )](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbjQuql%2FbtqDLFdIX2F%2FAAAAAAAAAAAAAAAAAAAAAE9XgBFRiUIh_DR1IMc4BeJ0V9Cvwi_Eh3gusDtv3-ml%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3DYv1QJYgfsIRaznLlRuZhpwDhSBg%253D)