나이브 베이즈 분류에 대해서 알아보기 전에 먼저 조건부 확률에 대해서 알아보자.
조건부 확률이란?
B가 주어졌을 때 사건 A의 조건부 확률 :

자료가 주어졌을 때 ( 조건을 주었을 때 ) 어떤 값의 확률을 뜻한다.
자세한 사항은 아래링크
2020/03/27 - [Data Science/Statistics] - [기초통계] 수학적 개념 ( 확률의 기초 , 확률 변수 , 확률 분포 )
[기초통계] 수학적 개념 ( 확률의 기초 , 확률 변수 , 확률 분포 )
확률 확률 실험 ( Random experiment): 다음과 같은 속성을 지닌 관찰이나 인위적인 실험 실험결과는 미리 알 수 없다. ( ex 주사위에서 뭐가 나올지 모른다 ) 실험에서 일어날 수 있는 모든 결과는
acdongpgm.tistory.com
베이즈 정리의 공식
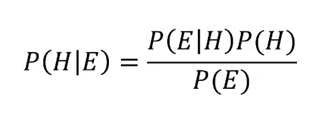
- 이 공식에는 네 개의 확률이 포함되어 있음. P(H|E) , P(E|H) , P(H) , P(E)
- 이 중 P(H)와 P(H|E)는 각각 사전 확률 , 사후 확률이라고 불림.
- 기본적으로 베이즈 정리는 사전확률과 사후 확률의 관계에 대해 설명하고 있음.
- 사전확률에 조건부 확률을 곱해서 사후확률을 갱신함
H : Hypothesis 가설 혹은 ' 어떤 사건이 발생했다는 주장'
E : Evidence ' 새로운 정보'
베이즈 정리를 잘 이해하지 못하는 이유
베이즈 정리는 통계학의 패러다임을 전환 시킴
연역적 추론에서 귀납적 추론으로
기존의 통계학 : 빈도 주의 ( frequentism )
- 연역적 사고에 기반
- 확률 계산, 유의성 검정
- 엄격한 확률 공간 정의하거나 집단의 분포를 정의하고 파생 결과물을 수용
새로운 통계학 : 베이지안주의 ( Bayesianism )
- 경험에 기반한 선험적인, 혹은 불확실성을 내포하는 수치를 기반으로 함
- 추가되는 정보를 바탕으로 사전 확률을 갱신함.
- 귀납적 추론 방법
- 추가 근거 확보를 통해 진리로 더 다가갈 수 있다는 철학을 내포.
- P(H)을 P(H|E)로 갱신한다.
나이브 베이즈 분류는 베이즈 정리를 통해 나온 값 P(H|E)을 비교하여 분류하는 것이다.
P(H) : 어떤 사건이 발생했다는 주장에 관한 신뢰도
P(H|E) : 새로운 정보를 받은 후 갱신된 신뢰도
즉 어떤 사건이 발생했을 때 새로운 정보의 확률과 기존의 새로운 정보와 관련 없는 확률의 곱으로 표현한 것
어떤 사건이 발생했을 때 새로운 정보의 확률과 사전확률의 곱
예를 들면
테니스를 날씨에 따라서 치는 사람도 있지만 날씨의 상관없이 테니스 자체를 많이 치는 사람(사전 확률)도 있다.

사전 확률에 사건을 계속해서 반영하여 갱신하는 것이 나이브 베이지 분류의 특징이라고 볼 수 있다.
공식을 이해하기 쉽게 풀어서 정리해보자.

위의 그림처럼 A1, ..... Ak 가 배반 사건(서로 교집합이 존재하지 않을 때)일 때.

위의 식처럼 조건부 확률을 정리할 때 P(B)를 각각 쪼개서 P(A1 n B) +.... + P(Ak n B)로 바꿔서 표현할 수 있다 ( 배반 사건이기 때문에) 그 다음 다시 P(Ai n B)의 식을 조건부 확률로 정리할 수 있다.

결과적으로 P(B|Ak) 은 조건부 확률이고 P(A1)은 사전 확률이다.
이 둘의 곱이 사후확률(Ai|B)이 된다.
분모의 해석 : P(B|A1)P(A1) + ... + P(B|Ak)P(Ak)
예를 들어 특정, 겉보기 날씨와 습도가 고정되어 있다고 할 때 , 가질 수 있는 패턴은 테니스를 치느냐 마느냐 두 가지 범주
( Yes or No )

이 확률이 분모에 해당이 된다.
P(B) = P(B n A1) + P(B n A2)
-> P(날씨 습도에 따른 테니스를 치는 확률) 이것을 쪼개면
날씨와 습도가 있을 때 테니스를 칠 확률 + 날씨와 습도가 있을 때 테니스를 안 칠 확률
분자의 해석 : P(B|Ai)P(Ai)
테니스를 많이 치는 경우와 테니스를 쳤을 때, 해당 날씨와 습도가 자주 출현한 경우의 곱이 분자의 해당이 된다.

P( Ai n B ) = P(B|Ai) x P(Ai)
P( 해당 날씨와 습도가 출현할 확률 | 테니스를 칠 확률 ) * P(테니스를 칠 확률)
조건부 확률과 사전 확률의 곱으로 표현된다.
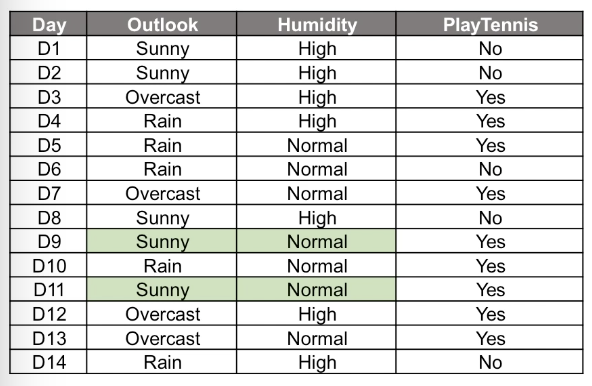
Sunny와 Normal 일 때 Yes일 확률은 1이다.
날씨가 맑음이고 습도가 보통일 때는 무조건 테니스를 친다!!
이건 그냥 확률적인 방법.
하지만
베이즈 정리 공식을 적용하면

위에서 보았던 식이 도출되고
여기서 분모 부분은 항상 고정이기 때문에 비교에 있어서는 필요가 없다.
( A 가 큰지 B 가 큰지 결정하는데 분모가 같으면 필요가 없다 )
분모 부분은 무시해도 좋다.
여기서 사전확률을 적용시켜 분자의 값을 구하고 Yes 인 경우와 No 인 경우의 각각의 값을 비교한다.

범주가 Yes 일 경우
P(Sunny, normal | Yes) = P(Sunny | Yes ) * P(normal | Yes ) = 2/9 * 6/9 = 4/27
알기 쉽게 글로 표현하면
- Yes 일 때 Sunny일 확률 곱하기 Yes일 때 normal 일 확률 = 4/27이다.
- Yes 일 경우 Sunny와 nomal 의 조건부 확률이 4/27이다.
- 테니스를 칠 경우 날씨가 맑을 때 확률 * 테니스를 칠 경우 습도가 보통일 때 확률 = 4/27 이다.
P(Yes) = 9/14
테니스를 칠 확률(사전 확률) = 9/14
P(Sunny, normal | Yes) * P(Yes) = 4/27 * 9/14 = 0.095
위 두 개를 곱한 값이 베이즈 정리의 분자 값이다. ( 분모는 필요 없음 )
범주가 No 일 경우
P(Sunny, normal | No ) * P(No) = 3/5 *1/5 * 5/14 = 0.043
No 일 경우 베이즈 정리의 분자 값.
NO일 경우와 YES 일 경우 두 개의 값을 비교해서 큰 값으로 예측한다.(분자의 비교)
YES ( 0.095 ) > NO ( 0.043 )
그래서 Sunny, normal 일 경우는 테니스를 칠 것(YES)이다라고 예측하게 되는 것이다.
범주가 많을 경우 많은 범주의 대응하는 값을 비교해서 제일 큰 값으로 예측한다.
이 과정이 나이브 베이즈 분류 ( Naive bayes classifier ) 알고리즘이다!!
'Machine learning' 카테고리의 다른 글
| [데이터 전처리] . 결측치 처리하기 ( Missing Values ) (0) | 2020.10.23 |
|---|---|
| [기계학습] KNN ( K-Nearest neighborhood ) k-최근접 이웃 (0) | 2020.07.09 |
| [기계학습]PCA (Principal Conponents Analysis) 주성분 분석 (0) | 2020.07.02 |
| [기계학습]회귀계수 축소법 ( Ridge regression, Ridge 회귀) (0) | 2020.06.25 |
| [기계학습] 변수 선택법 알고리즘( Python Code - 파이썬 예제 ) (0) | 2020.06.18 |
![[기계학습] 나이브 베이즈 분류 - Naive bayes classifier](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbwRdQt%2FbtqFvgPVH27%2FVSRfKW2VLyOYmvTqh99Gz0%2Fimg.png)