군집분석
군집내는 동질적이게 군집외는 이질적이게 하는 것
- 분석대상 상호관련성에 의해 설 동질적인 집단으로 그룹핑
- 사전에 집단이 모르는 자료를 유사한 것들끼리 분류하여 군집
- 비지도학습(목표변수 없음)
계층적 군집분석
유사한 개체를 묶어 나가는 과정을 반복하여 원하는 갯수의 군집을 형성
응집형(병합방법) : Bottom-up
하나의 군집이 남을 때 까지 순차적으로 군집들을 병합
(계층적 군집분석에는 주로 병합 방법이 쓰임)
분리형(분리방법) : Top - down
하나의 군집에서 n개 군집으로 분리
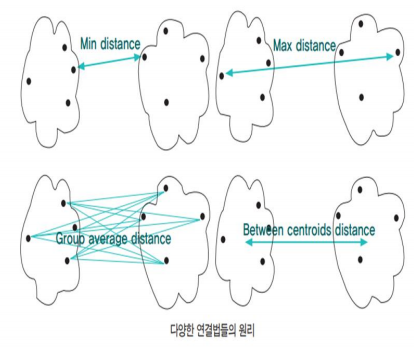
| 군집 방법 | 두 군집 사이의 거리 |
| 단일 연결법 (single linkage) |
한 군집의 점과 다른 군집의 점 사이의 가장 짧은 거리. ( 사슬 모양이 생길 수 있다.) |
| 완전 연결법 (complete linkage) |
각 군집에서 하나씩 관측값을 뽑았을 때 최댓값을 측정한다. 군집들의 내부 응집성에 중점을 둔 방법 |
| 평균연결법 (average linkage) |
모든 항복에 대한 거리 평균을 구하면서 군집화 ( 계산량이 불필요하게 많아질 수 있다.) |
| 중심연결법 (centroid) |
두 군집의 중심 간의 거리를 측정한다. ( 평균은 가중편균을 통해 구해진다. ) |
| 와드연결법 (Ward linkage) |
군집 내의 오차제곱합에 기초하여 군집을 수행한다. |
거리
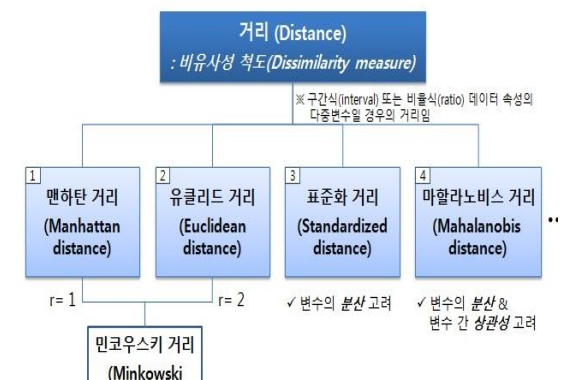
- 표준화 거리와 마할노비스 = 통계적거리
- 맨하탄 거리와 유클리드 거리 = 민코우스키 거리의 r 값에 따라 나뉜다.
- 유클리드의 일반화된 거리가 민코우스키 거리
캔버라 거리
- 가중치 있는 맨하탄 거리
코사인 유사도
- 두 벡터의 내적을 구한 값
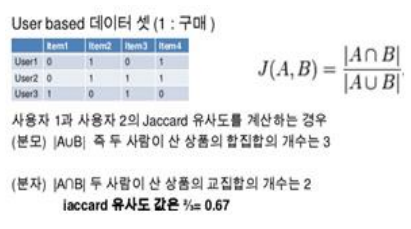
명목형 데이터에 대한 유사성 척도 : 자카드 계수
최단연결법 예제
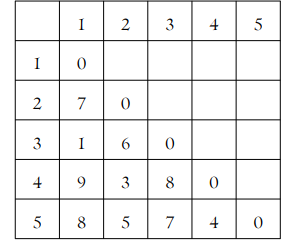
| 거리행렬에서 d(1,3)=1이 최소 관측값 1과 3을 묶어 군집 (1,3) 거리행렬을 갱신한다. d((1,3),2)=min{d(1,2),d(3,2)}=min{7,6}=6 d((1,3),4)=min{d(1,4),d(3,4)}=min{9,8}=8 d((1,3),5)=min{d(1,5),d(3,5)}=min{8,7}=7 |
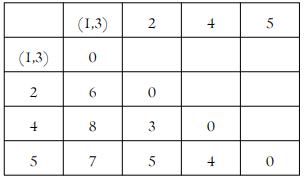
| 거리 행렬 갱신 d((1,3),(2,4))=min(d(1,3),2),d((1,3)),4)}=min{6,8}=6 d((2,4),5)=min(d(2,5)),d((4,5)}=min{5,4}=4 |
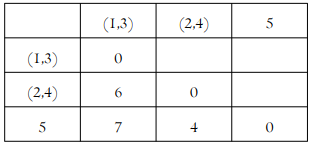
| d((2,4),5)=4 (2,4)와 5를 병합 |
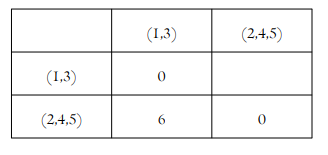
| d((1,3),(2,4,5))=min(d(1,3),(2,4),d((1,3)),5)}=min{6,7}=6 |
댄드로그램을 통해
- 무슨 군집과 무슨 군집이 서로 묶였는지
- 어떤 순서로 차례대로 묶였는지
- 군집 간 거리는 얼마나 되는지
알 수 있다.
계층적 군집의 장/단점
장점
- 군집의 수를 명시할 필요 없음
- 덴드로그램을 통해 군집화 결과를 표현하며 설명 및 해석이 가능
단점
- 데이터 집합이 매우 클 경우 계산 속도가 느림
- 이상치 값에 민감
계층적 군집 방법은 매 단계에서 지역적 최적화 수행하므로
그 결과가 전역적인 최적해라고 볼 수 없음.
병합적 방법에서 한 번 군집이 형성되면 군집에 속한 개체는 다른 군집으로 이동할 수 없다.
비계층적 군집분석
K-means 군집
- 초기에 군집수를 지정한다.(초기 군집수를 결정하기는 어렵다.) 몇 개가 적절한지 결정어렵다.
- 초기값을 너무 좁게하면 군집이 잘안되고 범위를 넓게하면 군집이 잘된다.
- 알고리즘이 단순하며 , 빠르게 수행된다.
- 중심점이 계속 이동하기 때문에 A 군집이 B로 바뀔 수 가 있다.
- 계층적군집보다 많은 양의 자료를 다룰 수 있다.
군집의 중심 계산하는 과정에 잡음이나 이상값에 영향을 많이 받는다.
이럴 경우 K 중앙값을 이용함. - 군집 내 오차제곱합의 합을 최소화 하는 것을 목적
- 오차 제곱합의 얼마나 군집화가 잘 되었는지를 알려주는 척도
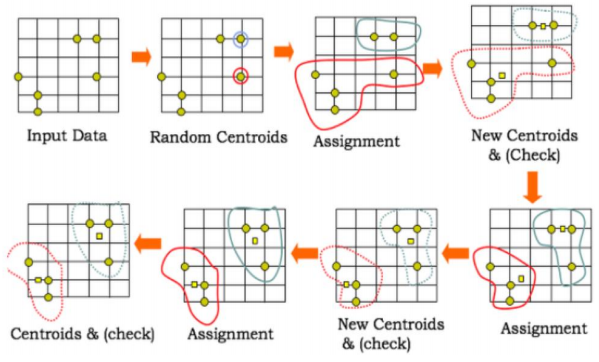
K-means 단계
| 군집의 개수 k 정한다. ( 계층적 군집과 다른 점) |
| 임의의 k개 점을 택하여 군집의 중심점으로 정한다. |
| 각 관찰치가 가장 가까운 중심점을 계산하여 특정한 중심점에 가까운 점들은 그 군에 속하는 것으로 간주 |
| 군집내의 점들의 평균을 계산하여 새로운 중심점 계산 |
| 중심점이 더이상 변화하지 않을 때 까지 3,4 과정 반복 |
혼합분포 군집
u 와 시그마를 초기값으로 지정한다.
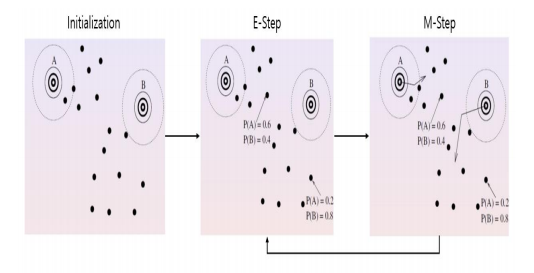
- 변수가 많고 분포함수가 많아지면 최대가능도 추정법으로 모수를 추정하기가 어렵다.
- E - Step ( 모수를 추정한 후 각 데이터 각각의 확률분포에 속할 확률을 계산한다.)
- M- Step (확률을 이용하여 최대가능도 추정법으로 모수의 추정을 다시한다.)
- 모수의 값이 변하지 않을 때 까지 반복 ( 평균과 분산이 계속 변동이 된다.)
혼합분포 군집 모형의 특징
- K-means 모형에 + 통계적 확률분포를 도입
- 서로 다른 크기나 모양의 군집을 찾을 수 있다.
- 군집을 몇개의 모수로서 표현할 수 있다.
- EM알고리즘은 데이터의 크기가 커지면 시간이 걸릴 수 있다.
- 한 군집의 크기가 너무 작으면 추정에 문제가 있을 수 있다.
- 잡음점이나 극단점에 민감한 결과를 가져 올 수 있다.
SOM(자기조직화지도)
인공신경망의 한 종류로 코호넨 네트워크 근간
주어진 입력 패턴에 정확한 해답을 주지 않고 자기 스스로 학습할 수 있는 능력
다차원의 데이터를 저차원으로 표현
| ANN | SOM |
| 연속적인 레이어 구성 | 뉴런(노드)2차원 그리드 구성 |
| 에러를 수정하는 방향으로 학습 | SOM은 경쟁학습 |
| 지도학습 | 비지도학습 |
| 역전파알고리즘(Back-propagation) | 한 번의 전방 전달(feedforward flow) |
SOM은 수치형 데이터 변수에만 사용이 가능 ( 범주형 자료를 더미변수로 변환 사용 )
경쟁학습(자율학습)이란?
입력벡터들을 신경회로망에 계속적으로 제시하면서 자율적으로 연결가중치를 변경
K-means 처럼 주어진 데이터를 k개의 클래스로 어느 오차수준 이하로 구분될 때 까지 반복
- 한 개의 입력층과 한 개의 출력층
- 입력층과 츨력층이 완전 연결
- 출력뉴런들은 승자 뉴런이 되기 위해 경쟁하고 오직 승자만이 학습함
- 입력벡터와 뉴런들 간의 거리를 측정할 때 유클리디언 거리를 사용한다.
- BMU와 BMU 이웃노드들만 연결가중치를 재조정한다.
- 첫 번째로 입력벡터와 뉴런들간의 연결강도를 임의의 값으로 초기화 한다.
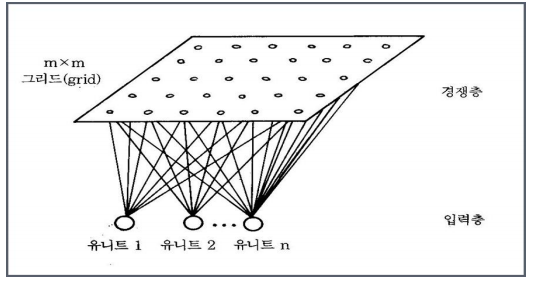
Input Layer 를 정규화(특정변수에 의해서 군집화 방지) 하고 Competitive Layer(경쟁층)을 0~1 값으로 초기화 해준다.
모든 연결은 입력층에서 경쟁층으로 연결
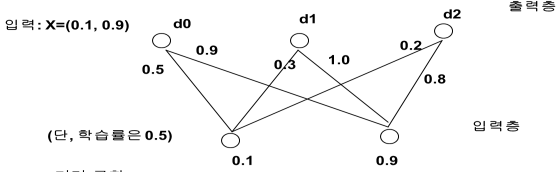
연결강도 벡터와 입력 벡터의 거리가 가장 가까운 뉴런만이 출력을 낼 수 있다.(승자 독점)
가장 가까운 노드를 BMU ( Best Matching Unit ) 이라고 한다.
위에 그림의 d2의 승자노드는 0.2
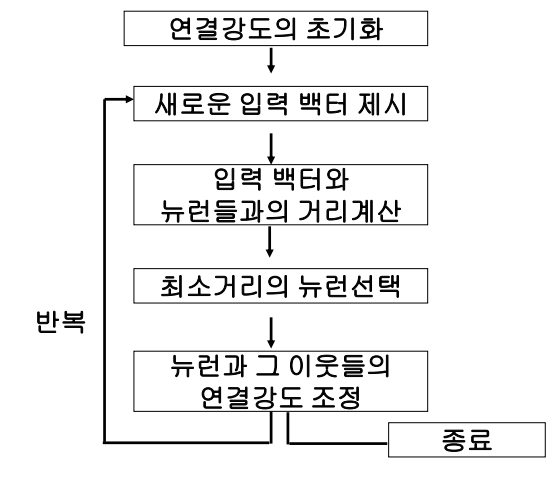
학습을 함에 따라서 이웃노드들의 범위가 작아지면서 군집화가 이루어짐
SOM 장점
구조상 수행이 상당히 빠른 모델이다.
- 전방패스(feedforward flow)를 사용하고 잠재적 실시간 학습 처리를 할 수 있기 때문
연속적인 학습이 가능하다.
입력데이터의 분포가 시간에 따라 변하면 코호넨 네트워크는 자동적으로 이런 변화에 적응
'Data Science > ADsP' 카테고리의 다른 글
| [ADsP]3과목 - 4장.연관분석 (0) | 2020.05.29 |
|---|---|
| [ADsP]3과목 - 4장.의사결정나무, 앙상블 모형 (0) | 2020.05.27 |
| [ADsP]3과목 - 4장.로지스틱회귀분석,신경망모형 (0) | 2020.05.27 |
| [ADsP]3과목 - 4장.데이터마이닝,모형평가 (0) | 2020.05.26 |
| [ADsP]3과목 - 3장.상관분석 및 다차원분석, 주성분분석,시계열 예측 (0) | 2020.05.26 |
![[ADsP]3과목 - 4장.군집분석,k평균군집,혼합분포군집,SOM(자기조직화지도)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fpox6y%2FbtqEuyYGMio%2FAAAAAAAAAAAAAAAAAAAAAANNy5mw5HXSirNYi6rOcxIbG0G3QUK_wwjV-2vMmSuj%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1769871599%26allow_ip%3D%26allow_referer%3D%26signature%3Da4uebKEetTRjH8AGg%252F7%252BjvcTrNA%253D)