[Machine Learning] 단순선형회귀분석(Simple Linear Regression) 예제 ,pandas , numpy , plot

SimpleLinearRegression.py

0.00MB

Machine Learning 머신러닝

 

먼저 회귀분석에 대해서 알아봅시다.

 

2020/04/22 - [데이터사이언스/머신러닝] - [기계학습] 4. 회귀분석 , 회귀계수 추정 , Matrix 미분 활용

[기계학습] 4. 회귀분석 , 회귀계수 추정 , Matrix 미분 활용

패키지 설치

import os import pandas as pd import numpy as np import statsmodels.api as sm cs

예제 실습을 하기 위해서 pandas , numpy , statsmodels 패키지를 설치해야합니다.

 

#현재경로 확인
print(os.getcwd())
 
#데이터 불러오기
boston = pd.read_csv("./실습/part2_data/Boston_house.csv")
 
#데이터 불러오기 확인
print(boston.head())
 
#target 제외한 데이터만 뽑기
boston_data = boston.drop(['Target'],axis=1)
 
#데이터 통계 보기
print(boston_data.describe())

 

head() : 맨 위에 5개의 데이터만 추출해주는 함수.

drop() : 해당데이터를 제거하는 함수 , 뒤에 파라미터는 행이나 열이나를 판단

describe() : 데이터의 통계를 총갯수 , 평균,  4분위로 보여줌.

 

describe() 결과

 

실습데이터 소개

타겟 데이터 1978 보스턴 주택 가격 506개 타운의 주택 가격 중앙값 ( 단위 1,000 달러 ) 특징데이터 CRIM : 볌죄율 INDUS : 비소매상업지역 면적 비율 NOX: 일산화질소 농도 RM: 주택당 방 수 LSTAT: 인구 중 하위 계층 비율 B: 인구 중 흑인 비율 PTRATIO: 학생/교사 비율 ZN: 25,000 평방피트를 초과 거주지역 비율 CHAS: 찰스강의 경계에 위차한 경우 1, 아니면 0 AGE: 1940년 이전에 건축된 주택의 비율 RAD: 방사형 고속도로까지의 거리 DIS: 직업센터의 거리 TAX: 재산세율

---

CRIM / RM / LSTAT 세개의 변수로 각각 단순 선형 회귀 분석하기

#타겟 설정
target = boston[['Target']]
crim = boston[['CRIM']]
rm = boston[['RM']]
lstat = boston[['LSTAT']]
 
#crim변수에 상수항추가하기
crim1 = sm.add_constant(crim,has_constant="add")
 
#sm.OLS 적합시키기
model1 = sm.OLS(target,crim1)
fitted_model1 = model1.fit()
 
#summary 함수통해 결과 출력
print(fitted_model1.summary())
 
#회귀 계수 출력
print(fitted_model1.params)

add_constatnt(crim,has_constant="add")

statsmodels에는상수항 결합을 위한 add_constant 함수가 제공된다.

 

OLS

OLS(Ordinary Least Squares)는 가장 기본적인 결정론적 선형 회귀 방법으로 잔차제곱합(RSS: Residual Sum of Squares)를 최소화하는 가중치 벡터를 행렬 미분으로 구하는 방법이다.

우리가 사용하는 예측 모형은 다음과 같이 상수항이 결합된 선형 모형이다.

 

 

fit() : 모델을 적합시키고 피팅해주는 것이다.

 

summary() : 회귀분석의 결과를 출력해주는 함수

summary() 함수 결과

---

#회귀 계수 x 데이터(x)
np.dot(crim1,fitted_model1.params)
pred1 = fitted_model1.predict()
 
#직접구한 yhat과 predict 함수를 통해 구한 yhat차이
print(np.dot(crim1,fitted_model1.params) - pred1)

params() : 회귀계수를 출력해주는 함수

predict() : yhat 을 구해주는 함수로 np.dot(crim1,fitted_model1.params)와 같다.

 

실제로 np.dot(crim1,fitted_model1.params) - pred1 를 해보면 모든 값이 0 인 행렬이 나온다.

* 차이가 없다는 뜻

 

#적합시킨 직선 시각화
import matplotlib.pyplot as plt
plt.yticks(fontname = "Arial")
plt.scatter(crim,target,label="data")
plt.plot(crim,pred1,label="result")
plt.legend()
plt.show()

 

 

plt.scatter(target,pred1)
plt.xlabel("real_value")
plt.ylabel("pred_value")
plt.show()cs

#residual 시각화
fitted_model1.resid.plot()
plt.xlabel("residual_number")
plt.show()cs

잔차그래프

 

잔차의 합 계산해보기

np.sum(fitted_model1.resid)cs

잔차의 합은 0 에 가깝게 나온다고 볼 수 있다.

Why? 

잔차가 최소한으로 하는 직선(선형회귀) OLS 를 적합시켰기 때문에

---

위와 동일하게 rm 변수와 lstat 변수로 각각 단순선형회귀분석 결과보기

#rm 모델결과출력
fitted_model2.summary()
 
#lstat 모델결과출력
fitted_model3.summary()
 
# 각각 yhat_예측하기
pred2 = fitted_model2.predict(rm1)
pred3 = fitted_model3.predict(lstat1)
 
#rm 시각화
plt.scatter(rm,target,label="data")
plt.plot(rm,pred2,label="result")
plt.legend()
plt.show()cs

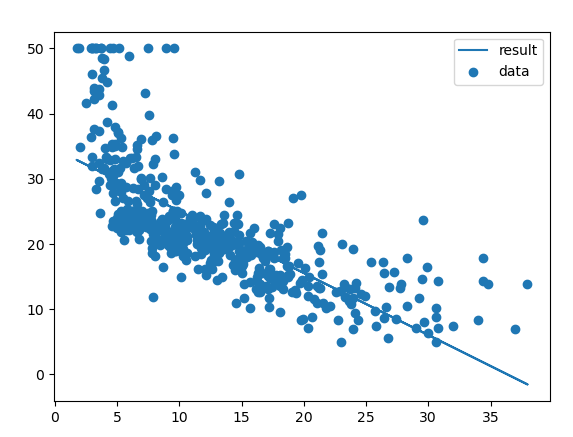
#lstat 시각화
plt.scatter(lstat,target,label="data")
plt.plot(lstat,pred3,label="result")
plt.legend()
plt.show()cs

#rm모델 residual시각화
fitted_model2.resid.plot()
plt.xlabel("residual_number")
plt.show()cs

#lstat모델 residual시각화
fitted_model3.resid.plot()
plt.xlabel("residual_number")
plt.show()cs

# 세 모델의 residual 비교 fitted_model1.resid.plot(label="crim") fitted_model2.resid.plot(label="rm") fitted_model3.resid.plot(label="lstat") plt.legend() plt.show() cs