[ADsP]3과목 - 2장.확률 및 확률분포 , 표본의 분포
통계학 : 수량적인 비교를 기초로 많은 사실을 관찰하고 분석하는 방법을 연구하는 학문
- 신뢰성 확보 , 의사결정에 근거, 문제해결을 위한 원인 파악
기술통계 : 표본에 대한 분석 결과의 각종 수치들을 활용하여 집단의 특성을 설명
- 자료의 요약 , EDA의 시각화
추론통계 : 표본을 활용하여 모집단의 특성을 나타내는 것
- 추정
모수 vs 통계량
모수(전수조사)
모수(Parameter) : 모집단을 분석하여 얻어지는 결과 수치
모평균, 모분산 , 모표준편차 , 모비율
통계량(표본조사)
통계량(Statistic) : 표본을 분석하여 얻어지는 결과 수치(통계치)
표본평균, 표본분산 ..
표본추출방법
확률적 표본추출
| 단순 무작위 추출 | 난수추출 |
| 계통 추출법 | 일정한 n개의 간격으로 표본추출 ,인터발 |
| 군집(집락)추출 | 내부 이질적이면서 외부 동질적으로 구성이라면 모집단 전체를 하지않고 몇개의 군집을 표본으로 선택해서 조사하는 방법 |
| 층화추출 | 각 계층(집단)을 대표할 수 있는 표본을 추출하는 방법 , 학년별 몇명씩 추출하는 방법 |
자료의 종류
통계학의 자료
질적변수
- 명목형 자료 : 분류를 목적으로 사용하는 자료
- 순위형 자료 : 순서로 분류할때 사용하는 자료
양적변수
- 이산형 자료 : 셀 수 있는 값을 나타낼 때 사용하는 자료
- 연속형 자료 : 측정 대상의 크기 변화가 연속적일 때 사용하는 자료 '절대 영점'이 존재한다.
| 변수 유형 | 자료 유형 | 인구주택총조사 결과 | 예 |
| 질적변수(범주형 자료) | 명목형(명목 척도) | 성별, 배우자와의 관계 | 거주지역 ,혈액형 등 |
| 순서형(서열 척도) | 학력 | 학점(A,B,C) | |
| 양적변수(수치형 자료) | 이산형(구간척도) | 출생아 수 | 형제 수 , 수강과목 수 , 온도 |
| 연속형(비율 척도) | 연령 | 키, 몸무게 |
확률 및 확률분포
표본공간
- 확률실험으로부터 출현 가능한 모든 결과들의 모임
- 예제 : 동전던지기
사건(Event) : 표본 공간의 각 원소들의 부분집합
근원사건 : 어떤 사건이 표본공간상의 하나의 원소로 구성된 사건
ex) 동전던지기 근원사건 {H} 와 {T}
확률 법칙
덧셈법칙
- 임의의 사건 A와 사건 B의 합사건에 대한 확률
- P(AUB) = P(A) + P(B) - P(AnB)
곱셈법칙
조건부 확률
두 사건 A와 B에 대해
- P ( A | B ) : 사건 B 가 발생했을 때 사건 A가 발생할 확률
- P( A | B ) = P(AnB) / P(B) B가 두개 들어감
- P ( B | A ) = P(AnB) / P(A) A가 두개 들어감
예시)
두사위를 던지는 실험에서 주사위의 눈이 짝수인 사건을 A,
주사위의 눈이 4이상인 사건을 B라 할 때 P(A|B)를 구해봅시다.
P(A|B) = P(AnB) / P(B) 이므로 P(B)와 P(AnB)를 구합니다.
P(B) : 주사위 눈이 4이상 나올 확률 = 1/2
P(AnB) : 주사위 눈이 짝수이고 4이상인 경우는 { 4 , 6 } 이므로 확률은 1/3

만일 두 사건 A와 B가 독립이라면
P(AnB) = P(A)P(B)
P(A|B) = P(A)
사건 A의 확률은 사건 B가 일어났는지 여부와 상관없이 동일하다.

이산형 확률 변수의 기대값

ex) 주사위를 던졌을 때의 기대값
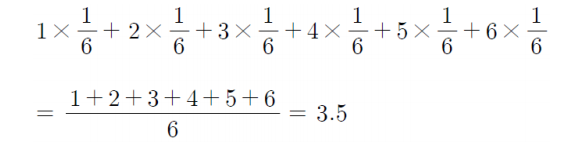
연속형 확률 변수의 기대값

확률변수의 분산
기대값의 특성을 나타내는 값

확률 변수들이 기대값으로부터 벗어나는 정도
이산형 확률분포 vs 연속형 확률분포
확률분포
확률변수가 취할 수 있는 값과 각 값이 나타날 확률을 대응시킨 관계
이산형 확률분포 : 베르누이 분포 , 이항분포, 초기화 분포, 포아송 분포
ex) 정수로 구분할 수 있는 경우 이산형 ex) 안경 쓴 학생수
연속형 확률분포 : 균등분포, 정규분포, t 분포 , 카이제곱분포 , F 분포
ex) 정수로 셀 수 없기 때문에 일정구간 설정 ex) 키 170~171 학생수
표본의 분포
표본을 추출한 후 , 표본의 특성을 파악하기 위해 표본분포의 확인이 필요
정규분포 : 중심(평균)을 기준으로 좌우가 대칭되는 분포
Z분포 (표준정규분포) : 평균이 = 0 , 분산이 = 1 인 정규분포
중심극한정리 :
표본의 개수가 30개 이상이라면 모수를 모르는 상황에서도 표본 통계량으로 정규분포를 구성하여 모수를 추정 가능
t분포 : 표본이 충분하지 못한 경우, 즉 표본의 개수가 30개를 넘지 못하는 경우에는 t 분포를 사용
30개가 넘는 경우에는 z 분포를 사용하고 표본의 갯수가 무한으로 갈때 z분포와 t분포는 동일한 분포가된다.

* n = 30로 맞추면 결측값이 있기 때문에 30개 이상으로 여유있게 표본의 갯수를 맞춰줘야한다.
X^2 분포 ( 카이제곱 분포)
: 정규분포로부터 도출되고, z분포의 제곱에 대한 분포 ( 항상 0보다 큰값)

F분포
: F분포는 두 개의 분산에 관한 추론 -> F(v1,v2)
v1 , v2 는 각각의 X^2(카이제곱 분포)에 대한 분산
F = v1/v2 는 각 비율을 나타냄
